久しく更新が滞ってしまいましたが、2016年の最後でこれまで続けていたQDAプロセスに関する連載をまとめたいと思います。
前回は、パネルのパフォーマンスの評価について書きましたが、サンプル間の差の有効性を結論づける際、交互作用の効果を知ることが大切です。交互作用は、繰り返し試験をした二元配置分散分析によって誤差項から分離することができます。つまり、1回だけの試験では明らかにできません(繰り返しの試験が、QDAの本質です!)
交互作用:相殺効果と相乗効果
交互作用には、相殺効果と相乗効果の2つのタイプ(下図)があり、パネリスト間の感度、または尺度の使い方に違いがあることを考えれば相乗効果に有意差が出ることはそれほど問題ではありません。もし相乗効果の交互作用があるときは、スコアを順位に変換して解析することもひとつの手段です。それに対して、相殺効果はサンプル間の順位の違いを反映するのでより解
釈に注意が必要です。
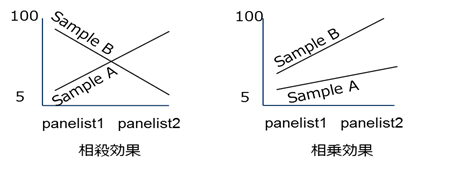
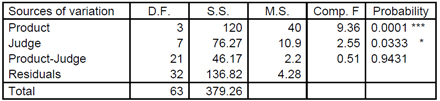
一般的なQDAデータの二元配置分散分析の一例を下表に示します。
分散分析でサンプルの効果に有意差が見つかったとき、どのサンプルに差があるかを確認するために多重比較検定を行います。多重比較検定には、Duncan、Newman‒Keuls、Scheffe、Tukey (a)、Tukey (b)、LSD、Dunnettなど多くの手法がありますが、主に第1種の過誤と第2種の過誤のどちらを重点的に保護するかを考慮し、選択することになります。前者ではTukey
が、後者ではDuncanがよく利用されています。
また、サンプル間の違いを視覚化するために利用されるのが、主成分分析です。属性間の相関を利用してQDAデータに含まれる多くの情報を抽出、集約する方法で、新しい2軸上にサンプルを分類し属性との関係をよりよく理解することができます。


